HDU 1325是有向图,给定某个节点是另一个元素的父节点 HDU 1272是无向图,将两个节点连接起来
共同点:判断是否成环,判断是树木还是森林
区别:有向图可能出现多个箭头指向同一个节点的情况(即一个节点多个父节点)
例如
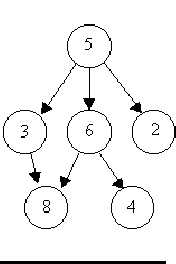
另外,关于HDU 1272
评论区看到一种利用离散数学结论的解法 (对于无向图) 如果m个节点被连成环,那么边的条数就是 m 如果m个节点形成了n个树,那么边的条数就是 m - n (这个动动笔画画就能明白) 链接:这题目干嘛都用并查集做啊 那么按照题目要求:Yes的条件就是 1.边的条数 = 所有节点数 - 1 或 2.节点数为0
上代码: HDU 1325
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#define maxlen 200005
using namespace std;
//并查集实现
int roots, ok;
int fa[maxlen];
// 这个栈和栈顶指针只是用来记录出现过的元素,用来清空fa数组用的,
// 记录fa数组的哪些地方被用过了,
// 完成一个示例以后就根据这个栈里面记录的位置来把fa数组里面对应的位置恢复成0
// 之所以不用memset,是因为fa数组很大,不是所有部分都用上了,每次都把整个数组写0太浪费时间了
int stack[maxlen];
int top = -1;
int find(int i) {//非递归实现
int icopy = i;
while (i != fa[i]) {//找到根元素
i = fa[i];
}
while (icopy != fa[icopy]) {
icopy = fa[icopy];//获取父节点
fa[icopy] = i;//挂到根节点下
}
return i;
}
int main(int argc, char const *argv[]) {
int a, b, t = 1;
int count = 0;
while (1) {
ok = 1;
count = 0;
// memset(fa, 0, sizeof(fa));//每次都全部写0,耗时长,改为用栈记录修改过的位置
while (scanf("%d%d", &a, &b) && a > 0 && b > 0) {
// a --> b
// a是b的父节点
if (ok) {
if (!fa[a]) { //若a没有出现过,就初始化为自己
fa[a] = a;
count++;
top++;
stack[top] = a;
// printf("add\n");
}
if (!fa[b]) {
fa[b] = b;
top++;
stack[top] = b;
} else {
if (fa[b] == b) {
count--;
// printf("sub\n");
}
}
if (fa[b] != b && fa[b] != a) {//若出现多指一,则不ok
ok = 0;
// printf("die 1\n");
continue;
} else {
a = find(a);//把a换为a的根节点
if (b == a) {//环
ok = 0;
// printf("die 2\n");
continue;
} else {
fa[b] = a;//直接挂在根节点
}
}
}
}
if (a < 0 && b < 0) {
break;
}
if (ok) {
if (count != 1) {
ok = 0;
// printf("die 3\n");
}
}
printf("Case %d is %sa tree.\n", t, ok ? "" : "not ");
while (top != -1) {
fa[stack[top]] = 0;
top--;
}
t++;
}
return 0;
}
HDU 1272
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#define maxlen 200005
using namespace std;
//并查集实现
//虽然给的输入似乎是无向的,但最终我们构造的依然是一个有向的树,我们只要考虑是否会出现环和森林,所以这题和hdu1325性质相同
int ok;
int fa[maxlen];
// 这个栈和栈顶指针只是用来记录出现过的元素,用来清空fa数组用的,
// 记录fa数组的哪些地方被用过了,
// 完成一个示例以后就根据这个栈里面记录的位置来把fa数组里面对应的位置恢复成0
// 之所以不用memset,是因为fa数组很大,不是所有部分都用上了,每次都把整个数组写0太浪费时间了
int stack[maxlen];
int top = -1;
int find(int i) {//非递归实现
int icopy = i;
while (i != fa[i]) {//找到根元素
i = fa[i];
}
while (icopy != fa[icopy]) {
icopy = fa[icopy];//获取父节点
fa[icopy] = i;//挂到根节点下
}
return i;
}
int main(int argc, char const *argv[]) {
int a, b;
int countOfRoots = 0;
while (1) {
ok = 1;
countOfRoots = 0;
// memset(fa, 0, sizeof(fa));//每次都全部写0,耗时长,改为用栈记录修改过的位置
while (scanf("%d%d", &a, &b) && a > 0 && b > 0) {
if (ok) {
if (!fa[a]) { //若a没有出现过,就初始化为自己
top++;
stack[top] = a;//所有出现过的节点都记录在stack中
if (!fa[b]) {//若b也没有出现过
top++;
stack[top] = b;
//指定a为b的父节点,a为独立的根节点
fa[a] = a;
fa[b] = a;
countOfRoots++;//根节点数量+1
} else {//若b出现过
fa[a] = find(b);//把a直接挂到b的根节点下
}
} else {//若a出现过
if (!fa[b]) {//而b没出现过
top++;
stack[top] = b;
fa[b] = find(a);//把b直接挂到a的根节点下
} else {//b也出现过
if (find(a) == find(b)) {//同一根节点
//成环
ok = 0;
} else {
// 把两个树合并
fa[find(a)] = find(b);
countOfRoots--;
}
}
}
}
}
if (a < 0 && b < 0) {
break;
}
if (ok) {
if (top != -1) {//排除掉一个元素都没有的情况(空树)
if (countOfRoots != 1) {
ok = 0;
}
}
}
printf("%s\n", ok ? "Yes" : "No");
while (top != -1) {
fa[stack[top]] = 0;
top--;
}
}
return 0;
}